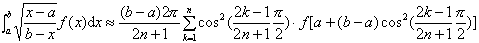八、积分的近似计算
1. 内插求积公式
[等距内插求积一般公式(柯斯特公式)]
![]() ≈(b-a)
≈(b-a)![]()
式中![]() 为等距节点:
为等距节点:
![]() =a+kh
k=0,1,2,…,n
=a+kh
k=0,1,2,…,n
![]()
![]() 为柯特斯系数(见下表).
为柯特斯系数(见下表).
柯特斯系数表
当区间[a,b]愈小,柯特斯公式所给出的结果愈精确.因此,当区间[a,b]较大时,为了避免采用n值较大的柯特斯公式,常把[a,b]N等分,对其中各个等份应用n值较小的柯特斯公式求积,然后再把各个等份的积分值相加,即得到区间[a,b]上的积分值,如下述的梯形公式(n=1)和辛卜生公式(n=2).
[梯形公式]
![]() ≈
≈![]()
![]() =a+kh,
k=1,2,…,N-1
=a+kh,
k=1,2,…,N-1
![]()
若![]() ≤M2,则截断误差为
≤M2,则截断误差为
![]() ≤
≤![]()
[辛卜生公式]
![]() ≈
≈![]()
![]() =a+k
=a+k![]() ,
,
![]()
若![]() ≤
≤![]() ,则截断误差为
,则截断误差为
![]() ≤
≤![]()
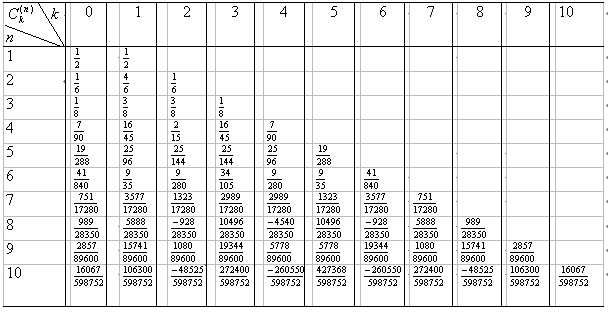
[龙贝公式] 设
![]()
![]()
=![]()
![]()
则
![]()
![]()
一般地,可适当选取m,使之固定,再增大k,使近似截断误差
![]()
在允许误差范围内即可,这时
![]() ≈
≈![]()
具体计算过程可按下表自左而右,自上而下进行(表中箭头方向表示计算顺序).
例 用龙贝公式计算积分
![]()
![]()
误差不超过0.0000001.
解 这里![]() ,a=0,b=1.可按五步进行计算,结果如下:
,a=0,b=1.可按五步进行计算,结果如下:
(1) ![]()
(2) ![]()
![]()
(3) ![]()
![]()
![]()
(4) ![]()
![]()
![]()
![]()
(5) 可以继续算出
![]() 3.140941614
3.140941614
![]() 3.141592655
3.141592655
![]() 3.141592665
3.141592665
![]() 3.141592643
3.141592643
因为
|![]() -
-![]() |=|3.141592643-3.141592665|<0.0000001
|=|3.141592643-3.141592665|<0.0000001
所以
![]() ≈3.14159264
≈3.14159264
而准确值为
![]()
![]()
在等距内插求积公式中,以辛卜生公式和龙贝公式为好,计算简单 ,便于在电子计算机上实现(都有标准程序),精确度也相当高.特别龙贝公式是采用区间逐次分半的方法,前一次分割得到的函数值在区间分半后仍可利用,具有计算有规律,不需存储柯特斯系数和节点等优点.
但等距内插求积公式不能计算广义积分.广义积分只能用下面的高斯型求积公式来计算.
[不等距内插求积公式(高斯型求积公式 )]
高斯型求积公式为
![]() ≈
≈![]() n=1,2,…
n=1,2,…
式中(a,b)区间可以是有限或无限,w(x)为(a,b)区间内的非负权函数.
-∞≤a≤![]() <
<![]() <…<
<…<![]() <b≤∞
<b≤∞
为求积节点(相应的正交多项式的根),![]() (k=1,2,…,n)为求积系数.f(x)为不超过2n-1次的多项式时,上述求积公式(1)成为等式.
(k=1,2,…,n)为求积系数.f(x)为不超过2n-1次的多项式时,上述求积公式(1)成为等式.
下面列出几种特例.
1°![]()
(-1<θ<1)
式中![]() 为勒让德多项式
为勒让德多项式![]() (见第十二章,§2,一)的根.
(见第十二章,§2,一)的根.
2°![]()
(-1<θ<1)
式中![]() 为第一类契贝谢夫多项式
为第一类契贝谢夫多项式![]() (见第十二章,§2,二)的根.
(见第十二章,§2,二)的根.
它也可表为
![]()
3°
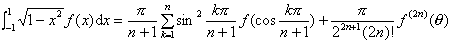
(-1<θ<1)
式中![]() 为第二类契贝谢夫多项式
为第二类契贝谢夫多项式![]() (见第十二章,§2,三)的根.
(见第十二章,§2,三)的根.
4°
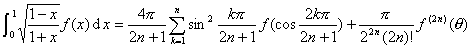
(-1<θ<1)
5°