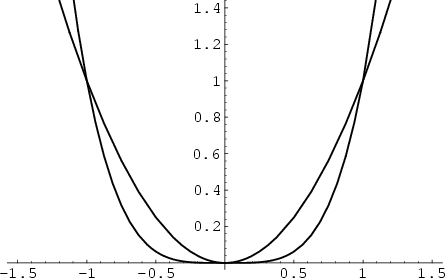
An osculating curve to 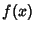 at
at 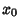 is tangent at that point and has the same Curvature. It therefore satisfies
is tangent at that point and has the same Curvature. It therefore satisfies
for 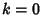 , 1, 2. The point of tangency is called a Tacnode. The simplest example of osculating curves are
, 1, 2. The point of tangency is called a Tacnode. The simplest example of osculating curves are 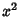 and
and
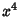 , which osculate at the point
, which osculate at the point 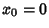 .
.
See also Tacnode
© 1996-9 Eric W. Weisstein
1999-05-26
![]() at
at ![]() is tangent at that point and has the same Curvature. It therefore satisfies
is tangent at that point and has the same Curvature. It therefore satisfies